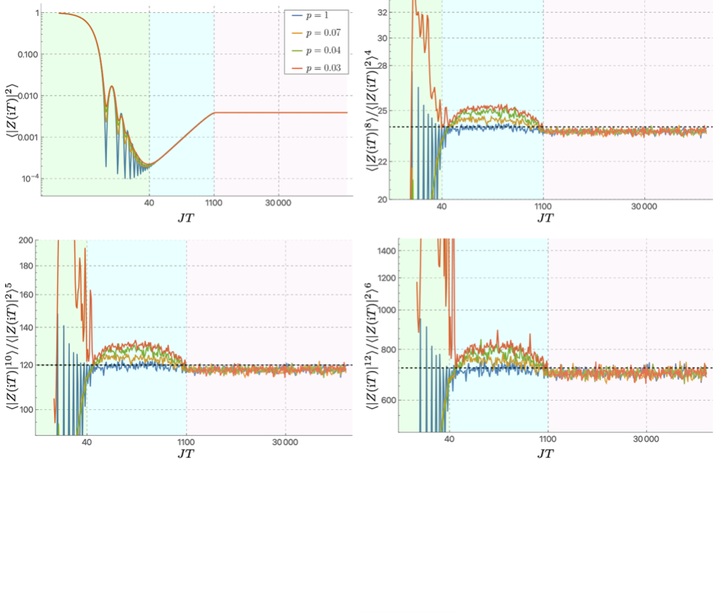
The spectral form factor and its moments for the sparse SYK. The plots correspond to the moments of order k=1, 4, 5, 6. Different colours represent different degrees of sparsification: p = 1 i.e. unsparsified SYK (blue), p = 0.07 (yellow), p = 0.04 (green), and p = 0.03 (red). The black dashed line marks the random matrix expectation equal to k!. In the ramp region (cyan background), the moments for regular SYK closely approach k!, while sparse SYK shows increasing deviations as sparsification increases.
Abstract
In chaotic quantum systems the spectral form factor exhibits a universal linear ramp and plateau structure with superimposed erratic oscillations. The mean signal and the statistics of the noise can be probed by the moments of the spectral form factor, also known as higher-point spectral form factors. We identify saddle points in the SYK model that describe the moments during the ramp region. Perturbative corrections around the saddle point indicate that SYK mimics random matrix statistics for the low order moments, while large deviations for the high order moments arise from fluctuations near the edge of the spectrum. The leading correction scales inversely with the number of random parameters in the SYK Hamiltonian and is amplified in a sparsified version of the SYK model, which we study numerically, even in regimes where a linear ramp persists. Finally, we study the q=2 SYK model, whose spectral form factor exhibits an exponential ramp with increased noise. These findings reveal how deviations from random matrix universality arise in disordered systems and motivate their interpretation from a bulk gravitational perspective.
