Engineering a $\mathrm{U}(1)$ lattice gauge theory in classical electric circuits

Abstract

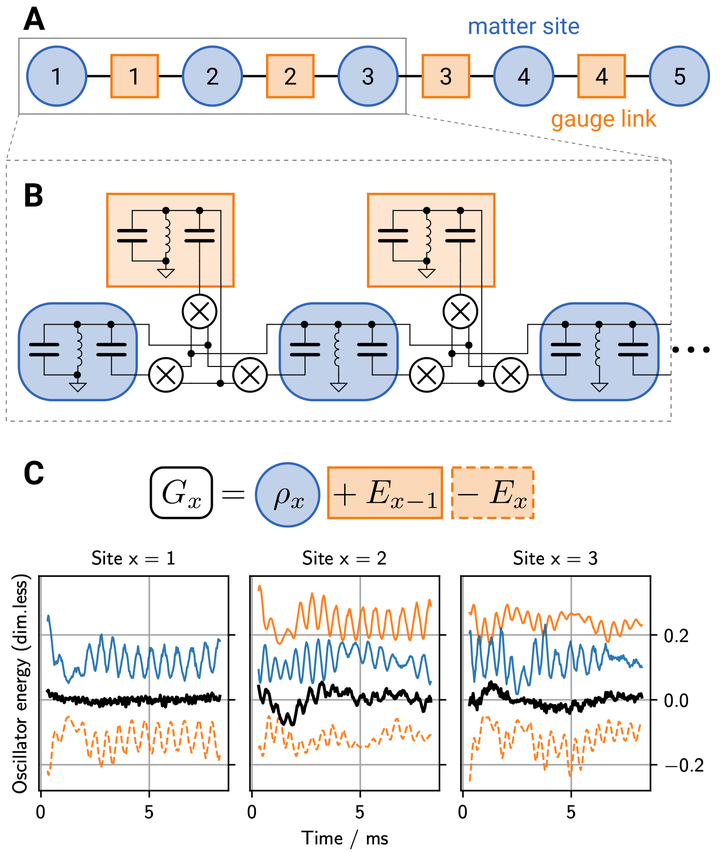
Lattice gauge theories are fundamental to such distinct fields as particle physics, condensed matter, and quantum information science. Their local symmetries enforce the charge conservation observed in the laws of physics. Impressive experimental progress has demonstrated that they can be engineered in table-top experiments using synthetic quantum systems. However, the challenges posed by the scalability of such lattice gauge simulators are pressing, thereby making the exploration of different experimental setups desirable. Here, we realize a $\mathrm{U}(1)$ lattice gauge theory with five matter sites and four gauge links in classical electric circuits employing nonlinear elements connecting LC oscillators. This allows for probing previously inaccessible spectral and transport properties in a multi-site system. We directly observe Gauss’s law, known from electrodynamics, and the emergence of long-range interactions between massive particles in full agreement with theoretical predictions. Our work paves the way for investigations of increasingly complex gauge theories on table-top classical setups, and demonstrates the precise control of nonlinear effects within metamaterial devices.