Gauge-Symmetry Violation Quantum Phase Transition in Lattice Gauge Theories
Abstract
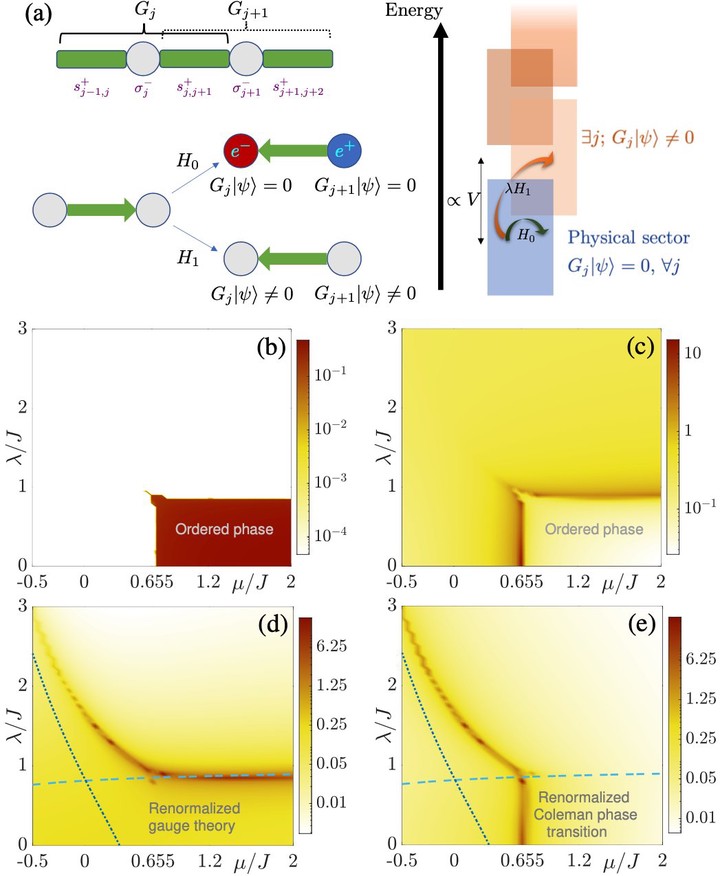
Gauge symmetry plays a key role in our description of subatomic matter. The vanishing photon mass, the long-ranged Coulomb law, and asymptotic freedom are all due to gauge invariance. Recent years have seen tantalizing progress in the microscopic reconstruction of gauge theories in engineered quantum simulators. Yet, many of these are plagued by a fundamental question: When gauge symmetry is only approximate in the quantum device, do we actually quantum-simulate a gauge theory? Here, we answer this question in the affirmative for a paradigm gauge theory akin to quantum electrodynamics. Analytically, we derive a renormalized gauge symmetry that is at least exponentially accurate. Further, numerically computing the phase diagram in the thermodynamic limit, we find that the long-distance behavior of the gauge theory is only compromised upon reaching a sharp quantum phase transition. This behavior is enabled by an energy penalty term, which lends a mass to the Higgs boson to which the coherent gauge breaking couples. Our results not only lend validity to ongoing gauge-theory quantum simulations, they also probe the fundamental question of how gauge symmetry could emerge in nature.

