Projective symmetry group classification of chiral $\mathbb{Z}_2$ spin liquids on the pyrochlore lattice: application to the spin-$1/2$ XXZ Heisenberg model

Abstract

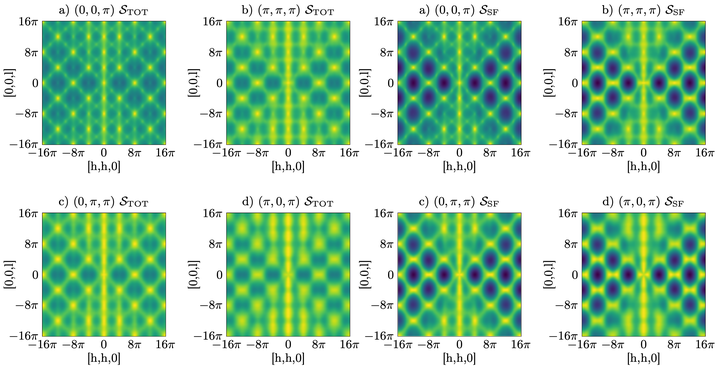
We give a complete classification of fully symmetric as well as chiral $\mathbb{Z}_2$ quantum spin liquids on the pyrochlore lattice using a projective symmetry group analysis of Schwinger boson mean-field states. We find $50$ independent ansätze, including the $12$ fully symmetric nearest-neighbor $\mathbb{Z}_2$ spin liquids that have been classified by Liu et al. [ Phys. Rev. B 100, 075125 (2019)]. For each class we specify the most general symmetry-allowed mean-field Hamiltonian. Additionally, we test the properties of a subset of the spin liquid ansätze by solving the mean-field equations for the spin-$1/2$ XXZ model near the antiferromagnetic Heisenberg point. We find that the ansatz with the lowest energy at mean-field level is a chiral spin liquid that breaks the screw symmetry of the lattice modulo time reversal symmetry. This state has a different symmetry than the previously studied monopole flux state. Moreover, this chiral spin liquid state has a substantially lower energy than all other symmetric spin liquid states, suggesting that it could be a stable ground state beyond the mean-field approximation employed in this work.