Quantum routing of information using chiral quantum walks

Abstract

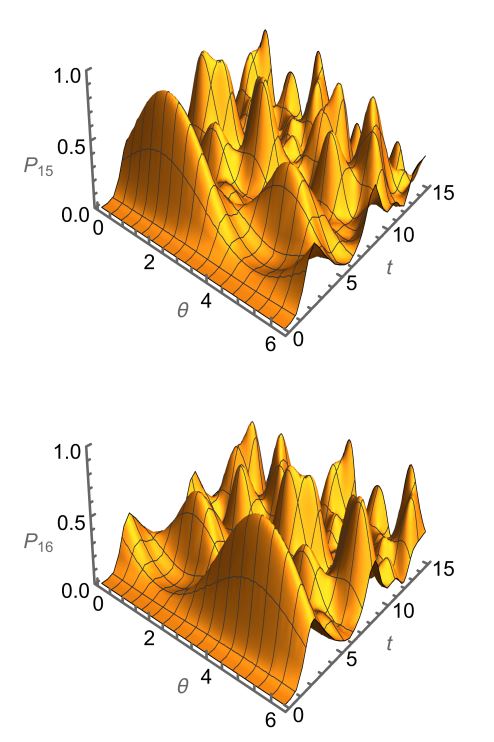
We address routing of classical and quantum information over quantum network and show how to exploit chirality (directionality) to achieve nearly optimal and robust transport. In particular, we prove how continuous-time chiral quantum walks over a minimal graph are able to model directional transfer of information over a network. At first, we show how classical information, encoded onto an excitation localized at one vertex of a simple graph, may be sent to any other chosen location with nearly unit fidelity by tuning a single phase. Then, we prove that high-fidelity transport is also possible for coherent superpositions of states, i.e., for routing of quantum information. Furthermore, we show that by tuning the phase parameter, one obtains universal quantum routing, i.e., independent on the input state. In our scheme, chirality is governed by a single phase, and the routing probability is robust against fluctuations of this parameter. Finally, we address characterization of quantum routers and show how to exploit the self-energies of the graph to achieve high precision in estimating the phase parameter.