Unconventional critical exponents at dynamical quantum phase transitions in a random Ising chain
Abstract
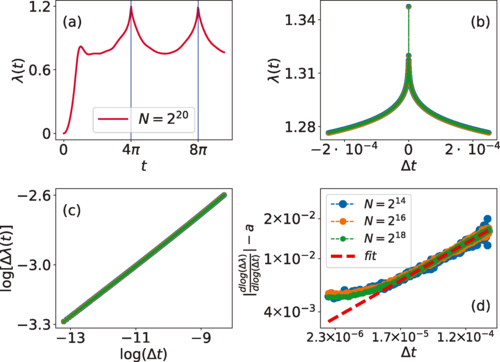
Dynamical quantum phase transitions (DQPTs) feature singular temporal behavior in transient quantum states during nonequilibrium real-time evolution. In this work we show that DQPTs in random Ising chains exhibit critical behavior with nontrivial exponents that are not integer valued and not of mean-field type. By means of an exact renormalization group transformation we estimate the exponents with high accuracy eliminating largely any finite-size effects. We further discuss how the considered dynamical phenomena can be made accessible in current Rydberg atom platforms. In this context we explore signatures of the DQPTs in the statistics of spin configuration measurements available in such architectures. Specifically, we study the statistics of clusters of consecutively aligned spins and observe a marked influence of the DQPT on the corresponding distribution.
Published 27 September 2021
