Achieving the quantum field theory limit in far-from-equilibrium quantum link models

Abstract

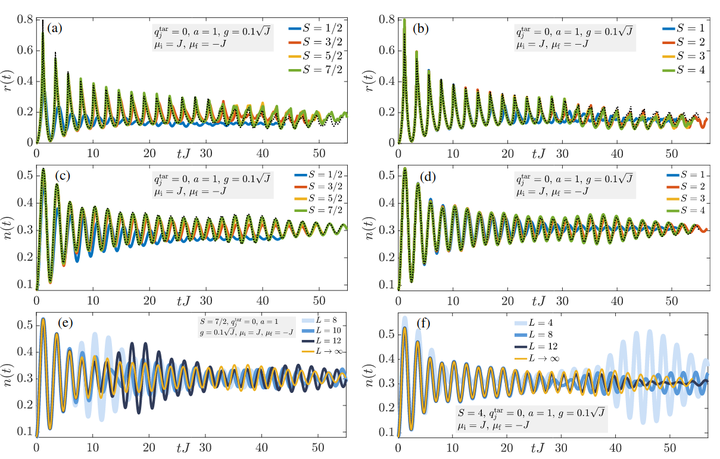
Realizations of gauge theories in setups of quantum synthetic matter open up the possibility of probing salient exotic phenomena in condensed matter and high-energy physics, along with potential applications in quantum information and science technologies. In light of the impressive ongoing efforts to achieve such realizations, a fundamental question regarding quantum link model regularizations of lattice gauge theories is how faithfully they capture the quantum field theory limit of gauge theories. Recent work [Zache, Van Damme, Halimeh, Hauke, and Banerjee, at this https URL] has shown through analytic derivations, exact diagonalization, and infinite matrix product state calculations that the low-energy physics of $1+1D$ $U(1)$ quantum link models approaches the quantum field theory limit already at small link spin length $S$. Here, we show that the approach to this limit also lends itself to the far-from-equilibrium quench dynamics of lattice gauge theories, as demonstrated by our numerical simulations of the Loschmidt return rate and the chiral condensate in infinite matrix product states, which work directly in the thermodynamic limit. Similar to our findings in equilibrium that show a distinct behavior between half-integer and integer link spin lengths, we find that criticality emerging in the Loschmidt return rate is fundamentally different between half-integer and integer spin quantum link models in the regime of strong electric-field coupling. Our results further affirm that state-of-the-art finite-size ultracold-atom and NISQ-device implementations of quantum link lattice gauge theories have the real potential to simulate their quantum field theory limit even in the far-from-equilibrium regime.