Enhancing disorder-free localization through dynamically emergent local symmetries

Abstract

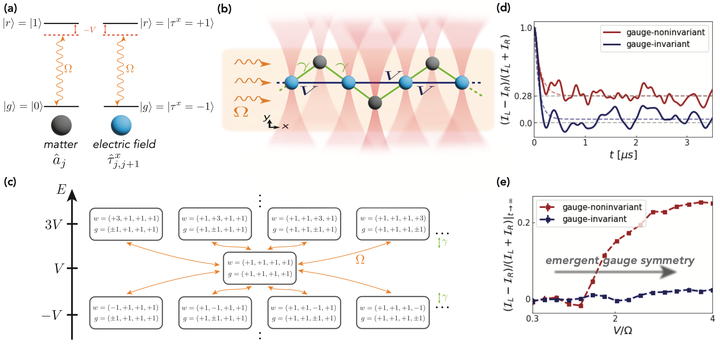
Disorder-free localization is a recently discovered phenomenon of nonergodicity that can emerge in quantum many-body systems hosting gauge symmetries when the initial state is prepared in a superposition of gauge superselection sectors. Thermalization is then prevented up to all accessible evolution times despite the model being nonintegrable and translation-invariant. In a recent work [Halimeh, Zhao, Hauke, and Knolle, arXiv:2111.02427], it has been shown that terms linear in the gauge-symmetry generator stabilize disorder-free localization in $U(1)$ gauge theories against gauge errors that couple different superselection sectors. Here, we show in the case of $\mathbb{Z}_2$ gauge theories that disorder-free localization can not only be stabilized, but also enhanced by the addition of translation-invariant terms linear in a local $\mathbb{Z}_2$ pseudogenerator that acts identically to the full generator in a single superselection sector, but not necessarily outside of it. We show analytically and numerically how this leads through the quantum Zeno effect to the dynamical emergence of a renormalized gauge theory with an enhanced local symmetry, which contains the $\mathbb{Z}_2$ gauge symmetry of the ideal model, associated with the $\mathbb{Z}_2$ pseudogenerator. The resulting proliferation of superselection sectors due to this dynamically emergent gauge theory creates an effective disorder greater than that in the original model, thereby enhancing disorder-free localization. We demonstrate the experimental feasibility of the $\mathbb{Z}_2$ pseudogenerator by providing a detailed readily implementable experimental proposal for the observation of disorder-free localization in a Rydberg setup.