Beyond braid statistics: Constructing a lattice model for anyons with exchange statistics intrinsic to one dimension
Abstract
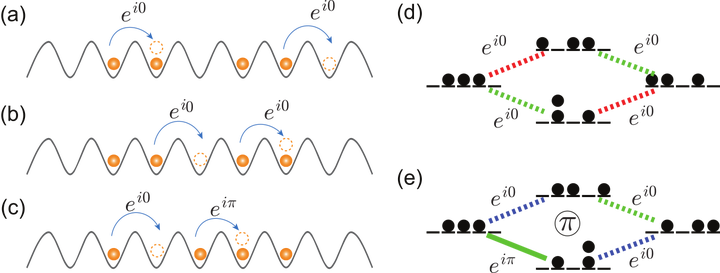
Anyons obeying fractional exchange statistics arise naturally in two dimensions: Hard-core two-body constraints make the configuration space of particles not simply-connected. The braid group describes how topologically-inequivalent exchange paths can be associated to non-trivial geometric phases for abelian anyons. Braid-anyon exchange statistics can also be found in one dimension (1D), but this requires broken Galilean invariance to distinguish different ways for two anyons to exchange. However, recently it was shown that an alternative form of exchange statistics can occur in 1D because hard-core three-body constraints also make the configuration space not simply-connected. Instead of the braid group, the topology of exchange paths and their associated non-trivial geometric phases are described by the traid group. In this article we propose a first concrete model realizing this alternative form of anyonic exchange statistics. Starting from a bosonic lattice model that implements the desired geometric phases with number-dependent Peierls phases, we then define anyonic operators so that the kinetic energy term in the Hamiltonian becomes local and quadratic with respect to them. The ground-state of this traid-anyon-Hubbard model exhibits several indications of exchange statistics intermediate between bosons and fermions, as well as signs of emergent approximate Haldane exclusion statistics. The continuum limit results in a Galilean invariant Hamiltonian with eigenstates that correspond to previously constructed continuum wave functions for traid anyons. This provides not only an a-posteriori justification of our lattice model, but also shows that our construction serves as an intuitive approach to traid anyons, i.e. anyons intrinsic to 1D.
Published 26 March 2024
