Entanglement Witnessing for Lattice Gauge Theories

Abstract

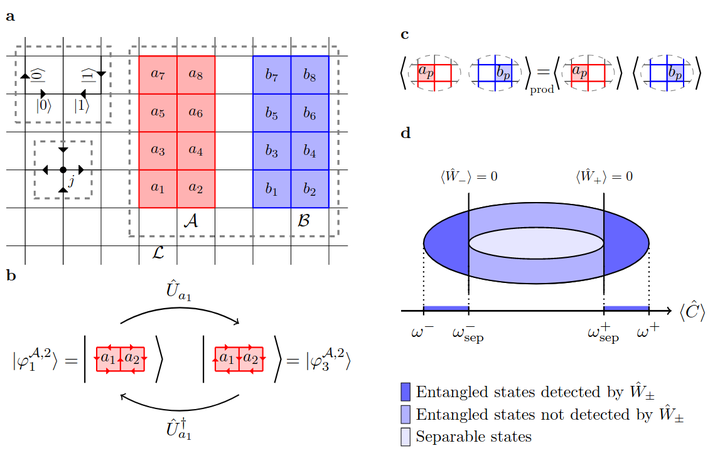
Entanglement is assuming a central role in modern quantum many-body physics. Yet, for lattice gauge theories its certification remains extremely challenging. A key difficulty stems from the local gauge constraints underlying the gauge theory, which separate the full Hilbert space into a direct sum of subspaces characterized by different superselection rules. In this work, we develop the theoretical framework of entanglement witnessing for lattice gauge theories that takes this subtlety into account. We illustrate the concept at the example of a $\mathrm{U}(1)$ lattice gauge theory in $2+1$ dimensions, without and with dynamical fermionic matter. As this framework circumvents costly state tomography, it opens the door to resource-efficient certification of entanglement in theoretical studies as well as in laboratory quantum simulations of gauge theories.