Probing confinement in a $\mathbb{Z}_2$ lattice gauge theory on a quantum computer

Abstract

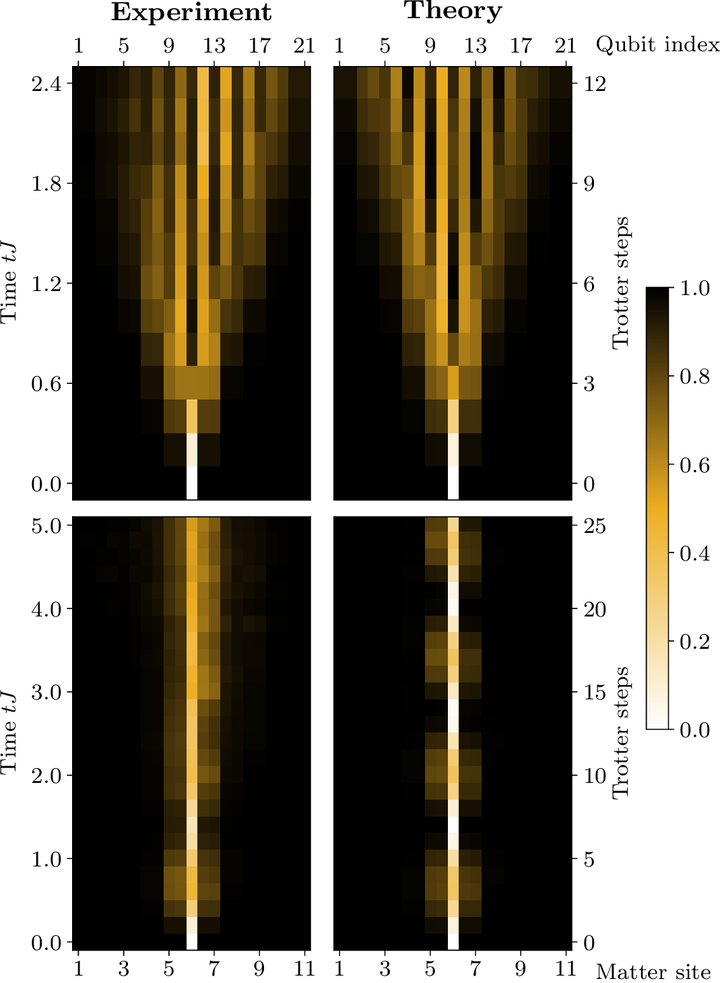
Digital quantum simulators provide a table-top platform for addressing salient questions in particle and condensed-matter physics. A particularly rewarding target is given by lattice gauge theories (LGTs). Their constituents, e.g., charged matter and the electric gauge field, are governed by local gauge constraints, which are highly challenging to engineer and which lead to intriguing yet not fully understood features such as confinement of particles. Here, we simulate confinement dynamics in a $\mathbb{Z}_2$ LGT on a superconducting quantum chip. We synthesize the charge–gauge-field interaction using only 6 native two-qubit gates, enabling us to reach simulation times of up to 25 Trotter steps. We observe how tuning a term that couples only to the electric field confines the charges, a manifestation of the tight bond that the local gauge constraint generates between both. Moreover, we study a different mechanism, where a modification of the gauge constraint from a $\mathbb{Z}_2$ to a $\mathrm{U}(1)$ symmetry freezes the system dynamics. Our work showcases the dramatic restriction that the underlying gauge constraint imposes on the dynamics of an LGT, it illustrates how gauge constraints can be modified and protected, and it paves the way for studying other models governed by many-body interactions.