Reliability of lattice gauge theories in the thermodynamic limit

Abstract

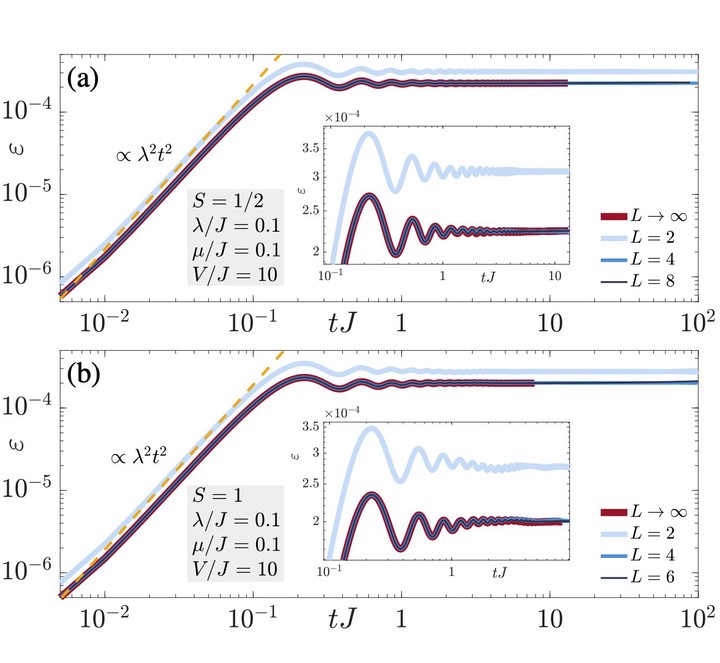
Although gauge invariance is a postulate in fundamental theories of nature such as quantum electrodynamics, in quantum-simulation implementations of gauge theories it is compromised by experimental imperfections. In a recent work [Halimeh and Hauke, Phys. Rev. Lett. 125, 030503 (2020)], it has been shown in finite-size spin-$1/2$ quantum link lattice gauge theories that upon introducing an energy-penalty term of sufficiently large strength $V$, unitary gauge-breaking errors at strength $\lambda$ are suppressed $\propto\lambda^2/V^2$ up to all accessible evolution times. Here, we show numerically that this result extends to quantum link models in the thermodynamic limit and with larger spin-$S$. As we show analytically, the dynamics at short times is described by an adjusted gauge theory up to a timescale that is at earliest $\tau_\text{adj}\propto\sqrt{V/V_0^3}$, with $V_0$ an energy factor. Moreover, our analytics predicts that a renormalized gauge theory dominates at intermediate times up to a timescale $\tau_\text{ren}\propto\exp(V/V_0)/V_0$. In both emergent gauge theories, $V$ is volume-independent and scales at worst $\sim S^2$. Furthermore, we numerically demonstrate that robust gauge invariance is also retained through a single-body gauge-protection term, which is experimentally straightforward to implement in ultracold-atom setups and NISQ devices.