Superfluidity and sound propagation in disordered Bose gases
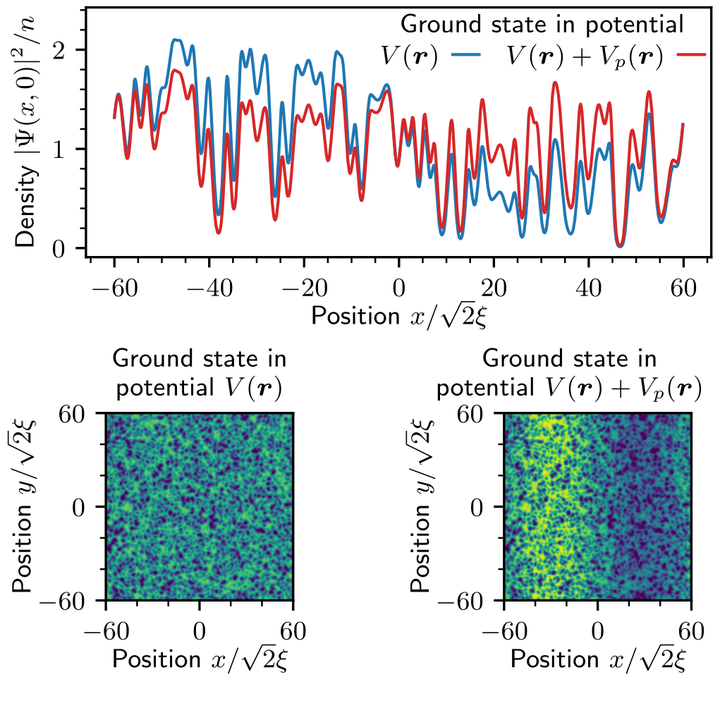 Linear-response protocol for probing sound propagation in a disordered Bose–Einstein condensate: a sound wave is excited by suddenly releasing a sinusoidal probe potential $V_p(\mathbf{r})$.
Linear-response protocol for probing sound propagation in a disordered Bose–Einstein condensate: a sound wave is excited by suddenly releasing a sinusoidal probe potential $V_p(\mathbf{r})$.
Abstract
Superfluidity describes the ability of quantum matter to flow without friction. Due to its fundamental role in many transport phenomena, it is crucial to understand the robustness of superfluid properties to external perturbations. Here, we theoretically study the effects of speckle disorder on the propagation of sound waves in a two-dimensional Bose–Einstein condensate at zero temperature. We numerically solve the Gross–Pitaevskii equation in the presence of disorder and employ a superfluid hydrodynamic approach to elucidate the role of the compressibility and superfluid fraction in the propagation of sound. A key result is that disorder reduces the superfluid fraction and hence the speed of sound; it also introduces damping and mode coupling. In the limit of weak disorder, the predictions for the speed of sound and its damping rate are well reproduced by a quadratic perturbation theory. The hydrodynamic description is valid over a wide range of parameters, while discrepancies become evident if the disorder becomes too strong, the effect being more significant for disorder applied in only one spatial direction. Our predictions are well within the reach of state-of-the-art cold-atom experiments and carry over to more general disorder potentials.
