Ground-state phase diagram of quantum link electrodynamics in $(2+1)$-d

Abstract

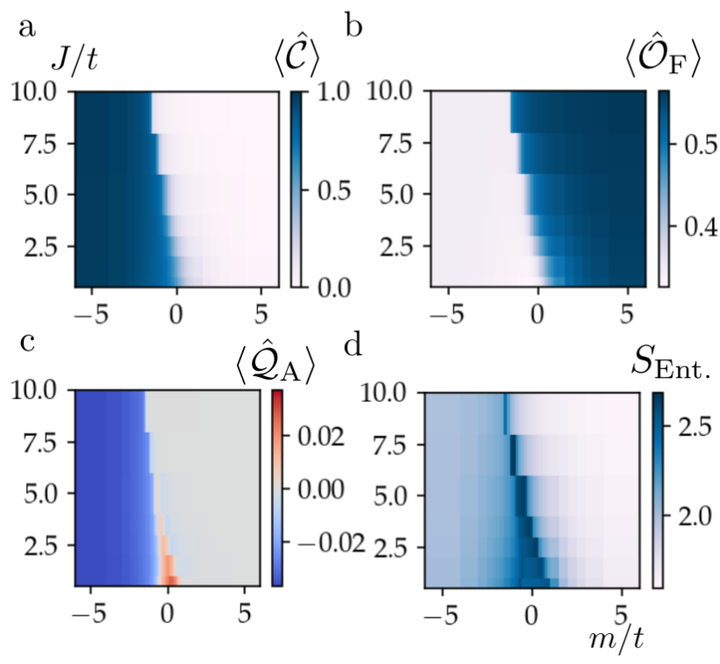
The exploration of phase diagrams of strongly interacting gauge theories coupled to matter in lower dimensions promises the identification of exotic phases and possible new universality classes, and it facilitates a better understanding of salient phenomena in Nature, such as confinement or high-temperature superconductivity. The emerging new techniques of quantum synthetic matter experiments as well as efficient classical computational methods with matrix product states have been extremely successful in one spatial dimension, and are now motivating such studies in two spatial dimensions. In this work, we consider a $U(1)$ quantum link lattice gauge theory where the gauge fields, represented by spin-$12$ operators are coupled to a single flavor of staggered fermions. Using matrix product states on infinite cylinders with increasing diameter, we conjecture its phase diagram in $(2+1)$-d. This model allows us to smoothly tune between the $U(1)$ quantum link and the quantum dimer models by adjusting the strength of the fermion mass term, enabling us to connect to the well-studied phases of those models. Our study reveals a rich phase diagram with exotic phases and interesting phase transitions to a potential liquid-like phase. It thus furthers the collection of gauge theory models that may guide future quantum-simulation experiments.