Observation of microscopic confinement dynamics by a tunable topological $\theta$-angle
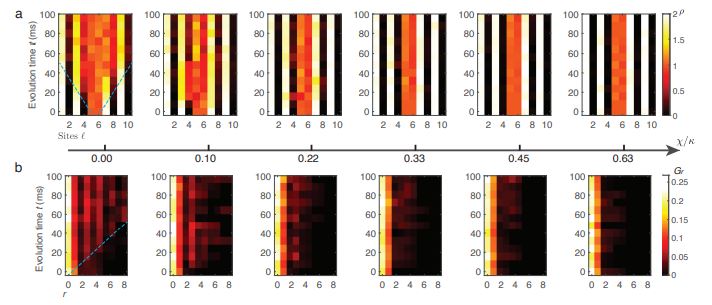 Evolution of densities and two-point correlations along a tunable topological $\theta$-angle.
Evolution of densities and two-point correlations along a tunable topological $\theta$-angle.
Abstract
The topological $\theta$-angle is central to the understanding of a plethora of phenomena in condensed matter and high-energy physics such as the strong CP problem, dynamical quantum topological phase transitions, and the confinement–deconfinement transition. Difficulties arise when probing the effects of the topological $\theta$-angle using classical methods, in particular through the appearance of a sign problem in numerical simulations. Quantum simulators offer a powerful alternate venue for realizing the $\theta$-angle, which has hitherto remained an outstanding challenge due to the difficulty of introducing a dynamical electric field in the experiment. Here, we report on the experimental realization of a tunable topological $\theta$-angle in a Bose–Hubbard gauge-theory quantum simulator, implemented through a tilted superlattice potential that induces an effective background electric field. We demonstrate the rich physics due to this angle by the direct observation of the confinement–deconfinement transition of $(1+1)$-dimensional quantum electrodynamics. Using an atomic-precision quantum gas microscope, we distinguish between the confined and deconfined phases by monitoring the real-time evolution of particle–antiparticle pairs, which exhibit constrained (ballistic) propagation for a finite (vanishing) deviation of the $\theta$-angle from $\pi$. Our work provides a major step forward in the realization of topological terms on modern quantum simulators, and the exploration of rich physics they have been theorized to entail.
