Polymer Physics by Quantum Computing

Abstract

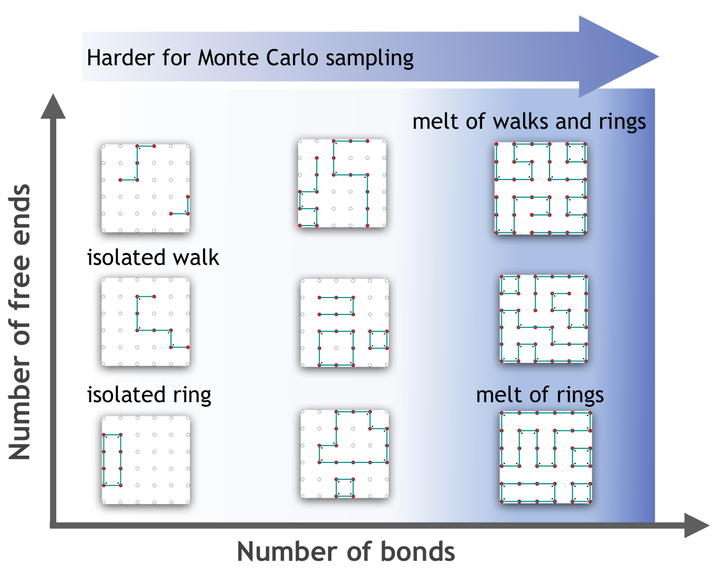
Sampling equilibrium ensembles of dense polymer mixtures is a paradigmatically hard problem in computational physics, even in lattice-based models. Here, we develop a formalism based on interacting binary tensors that allows for tackling this problem using quantum annealing machines. Our approach is general in that properties such as self-avoidance, branching, and looping can all be specified in terms of quadratic interactions of the tensors. Microstates realizations of different lattice polymer ensembles are then seamlessly generated by solving suitable discrete energy-minimization problems. This approach enables us to capitalize on the strengths of quantum annealing machines, as we demonstrate by sampling polymer mixtures from low to high densities, using the D-Wave quantum computer. Our systematic approach offers a promising avenue to harness the rapid development of quantum computers for sampling discrete models of filamentous soft-matter systems.