Quantum Resources in Non-Abelian Lattice Gauge Theories: Nonstabilizerness, Multipartite Entanglement, and Fermionic Non-Gaussianity
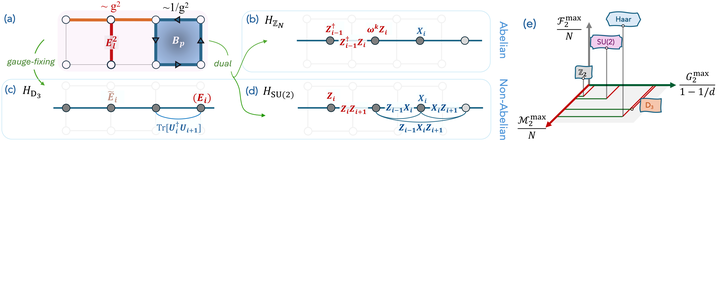 Sketch of the (2+1)D LGT flux ladder and the three different mappings to one-dimensional chains, depending on the underlying gauge symmetry: (b) ZN , (c) D3, (d) SU(2). (e) Sketch of the maximum values of the resources across the phase diagrams of the different models we consider: Multipartite entanglement G2, stabilizer Renyi entropy M2, and fermionic antiflatness F2. All values except the maximal GGM for D3 remain below those of Haar random states (fermionic antiflatness is not computed for D3).
Sketch of the (2+1)D LGT flux ladder and the three different mappings to one-dimensional chains, depending on the underlying gauge symmetry: (b) ZN , (c) D3, (d) SU(2). (e) Sketch of the maximum values of the resources across the phase diagrams of the different models we consider: Multipartite entanglement G2, stabilizer Renyi entropy M2, and fermionic antiflatness F2. All values except the maximal GGM for D3 remain below those of Haar random states (fermionic antiflatness is not computed for D3).
Abstract
Lattice gauge theories (LGTs) represent one of the most ambitious goals of quantum simulation. From a practical implementation perspective, non-Abelian theories present significantly tougher challenges than Abelian LGTs. However, it is unknown whether this is also reflected in increased values of quantum resources relating to the complexity of simulating quantum many-body models. Here, we compare three paradigmatic measures of quantum resources – stabilizer Rényi entropy, generalized geometric measure of entanglement, and fermionic antiflatness – for pure-gauge theories on a ladder with Abelian Z2 as well as non-Abelian D3 and SU(2) gauge symmetries. We find that non-Abelian symmetries are not necessarily inherently harder to simulate than Abelian ones, but rather the required quantum resources depend nontrivially on the interplay between the group structure, superselection sector, and encoding of the gauge constraints. Our findings help indicate where quantum advantage could emerge in simulations of LGTs, both in NISQ and fault-tolerant eras.





