Quantum Computation of Thermal Averages for a Non-Abelian D4 Lattice Gauge Theory via Quantum Metropolis Sampling
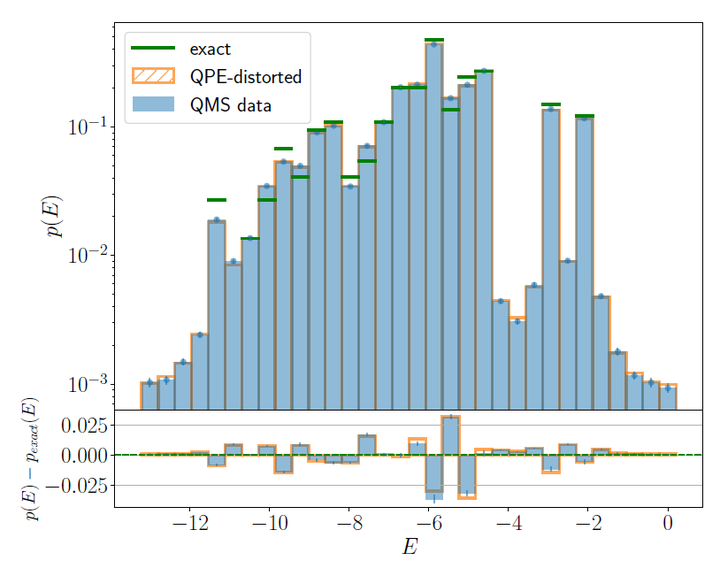Sampling at $\beta=0$ of the energy spectrum represented by 5 qubits.
Abstract
In this paper, we show the application of the Quantum Metropolis Sampling (QMS) algorithm to a toy gauge theory with discrete non-Abelian gauge group $D_4$ in (2+1)-dimensions, discussing in general how some components of hybrid quantum-classical algorithms should be adapted in the case of gauge theories. In particular, we discuss the construction of random unitary operators which preserve gauge invariance and act transitively on the physical Hilbert space, constituting an ergodic set of quantum Metropolis moves between gauge invariant eigenspaces, and introduce a protocol for gauge invariant measurements. Furthermore, we show how a finite resolution in the energy measurements distorts the energy and plaquette distribution measured via QMS, and propose a heuristic model that takes into account part of the deviations between numerical results and exact analytical results, whose discrepancy tends to vanish by increasing the number of qubits used for the energy measurements.
