Simulations of the dynamics of quantum impurity problems with matrix product states

Abstract

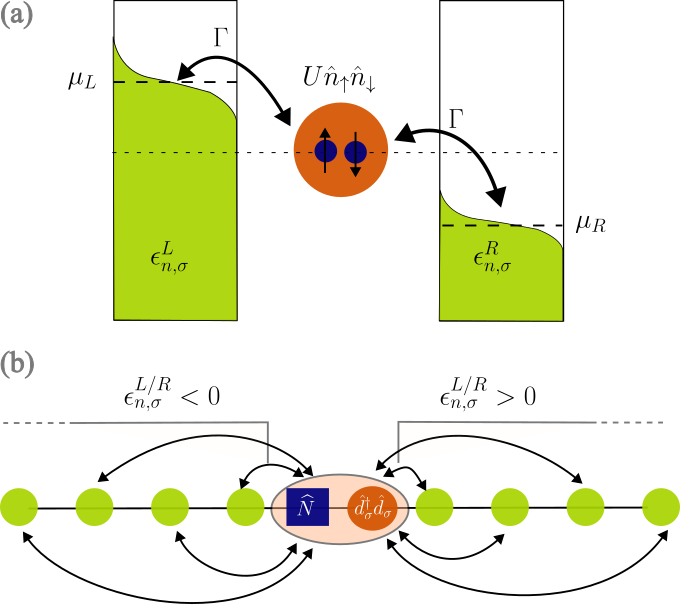
The Anderson impurity model is a paradigmatic example in the study of strongly correlated quantum systems and describes an interacting quantum dot coupled to electronic leads. Here we investigate its dynamics following a quantum quench based on matrix product state simulations. We examine the behavior of its impurity magnetization. Its relaxation allows us to extract the predicted scaling of the Kondo temperature as a function of the impurity-lead hybridization and quantum dot repulsion. Additionally, our simulations provide estimates of the currents in the nonequilibrium quasisteady state appearing after the quench. Through their values, we examine the dependence of the conductance on the voltage bias $V_b$ and on the impurity chemical potential $V_g$, which displays a zero-bias Kondo peak. Our results are relevant for transport measurements in Coulomb blockaded devices, and, in particular, in quantum dots induced in nanowires.