Universal equilibration dynamics of the Sachdev-Ye-Kitaev model
Abstract
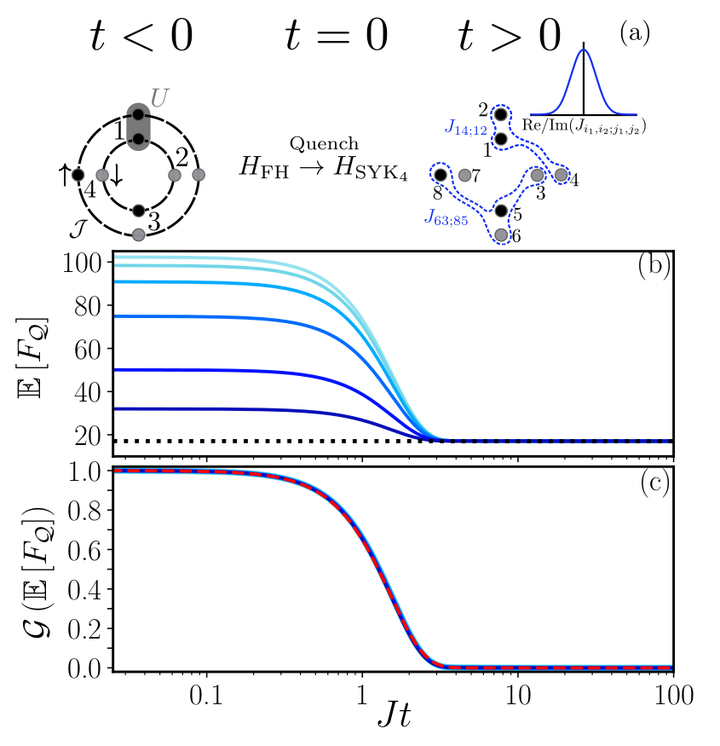
Equilibrium quantum many-body systems in the vicinity of phase transitions generically manifest universality. In contrast, limited knowledge has been gained on possible universal characteristics in the non-equilibrium evolution of systems in quantum critical phases. In this context, universality is generically attributed to the insensitivity of observables to the microscopic system parameters and initial conditions. Here, we present such a universal feature in the equilibration dynamics of the Sachdev-Ye-Kitaev (SYK) Hamiltonian – a paradigmatic system of disordered, all-to-all interacting fermions that has been designed as a phenomenological description of quantum critical regions. We drive the system far away from equilibrium by performing a global quench, and track how its ensemble average relaxes to a steady state. Employing state-of-the-art numerical simulations for the exact evolution, we reveal that the disorder-averaged evolution of few-body observables, including the quantum Fisher information and low-order moments of local operators, exhibit within numerical resolution a universal equilibration process. Under a straightforward rescaling, data that correspond to different initial states collapse onto a universal curve, which can be well approximated by a Gaussian throughout large parts of the evolution. To reveal the physics behind this process, we formulate a general theoretical framework based on the Novikov–Furutsu theorem. This framework extracts the disorder-averaged dynamics of a many-body system as an effective dissipative evolution, and can have applications beyond this work. The exact non-Markovian evolution of the SYK ensemble is very well captured by Bourret–Markov approximations, which contrary to common lore become justified thanks to the extreme chaoticity of the system, and universality is revealed in a spectral analysis of the corresponding Liouvillian.
Published 24 May 2023



