Symmetry-protection Zeno phase transition in monitored lattice gauge theories

Abstract

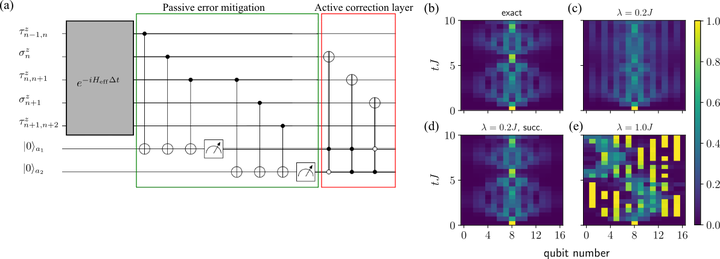
Quantum measurements profoundly influence system dynamics. They lead to complex nonequilibrium phenomena like the quantum Zeno effect, and they can be used for mitigating errors in quantum simulations. Such an ability is particularly valuable for lattice gauge theories (LGTs), which require the challenging preservation of an extensive number of local conservation laws. While it is known that tailored quantum measurements can soften violations of gauge symmetry, the nature of this protection, and in particular the possibility of a threshold behavior, is still unexplored. Here, we demonstrate the existence of a sharp transition, triggered by the measurement rate, between a protected gauge-theory regime resistant to simulation errors and an irregular regime. Our results are based on the paradigmatic example of a 1+1d Z2 LGT. We study in detail the protection through projective measurements of ancillary qubits coupled to the local symmetry generators, and compare this approach with analog (weak) measurement protocols. We show that, while the resulting ensemble averages in the continuous-time limit share the same Liouvillian dynamics, different physical implementations of the stochastic gauge protection protocol yield trajectory unravelings with vastly different statistics. Additionally, we design an on-chip feedback mechanism that corrects bit-flip errors and significantly enhances the discrete-time scheme. Our results shed light on the dissipative criticality of strongly-interacting, highly-constrained quantum systems, and they offer valuable insights into error mitigation and correction of gauge-theory quantum simulations.