Unraveling the emergence of quantum state designs in systems with symmetry

Abstract

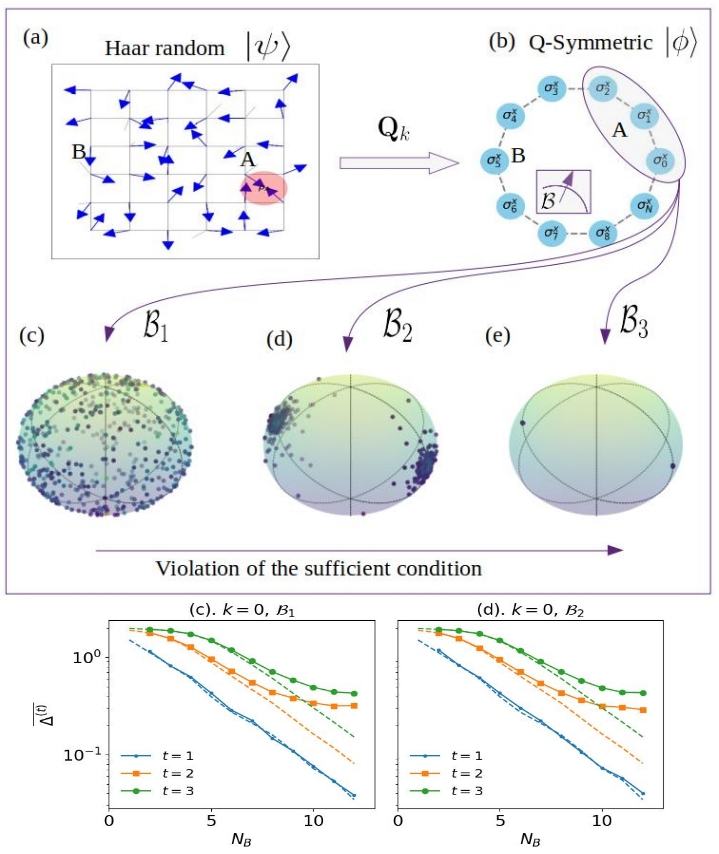
Quantum state designs, by enabling an efficient sampling of random quantum states, play a quintessential role in devising and benchmarking various quantum protocols with broad applications ranging from circuit designs to black hole physics. Symmetries, on the other hand, are expected to reduce the randomness of a state. Despite being ubiquitous, the effects of symmetries on the quantum state designs remain an outstanding question. The recently introduced projected ensemble framework generates efficient approximate state t-designs by hinging on projective measurements and many-body quantum chaos. In this work, we examine the emergence of state designs from the random generator states exhibiting symmetries. Leveraging on translation symmetry, we analytically establish a sufficient condition for the measurement basis leading to the state t-designs. Then, by making use of a trace distance measure, we numerically investigate the convergence to the designs. Subsequently, we inspect the violation of the sufficient condition to identify bases that fail to converge. We further demonstrate the emergence of state designs in a physical system by studying dynamics of a chaotic tilted field Ising chain with periodic boundary conditions. We find faster convergence of the trace distance in the initial time, however, it saturates to a finite value deviating from random matrix prediction at late times, in contrast to the case with open boundary condition. To delineate the general applicability of our results, we extend our analysis to other symmetries. We expect our findings to pave the way for further exploration of deep thermalization and equilibration of closed and open quantum many-body systems.