Generalized Discrete Truncated Wigner Approximation for Nonadiabtic Quantum-Classical Dynamics

Abstract

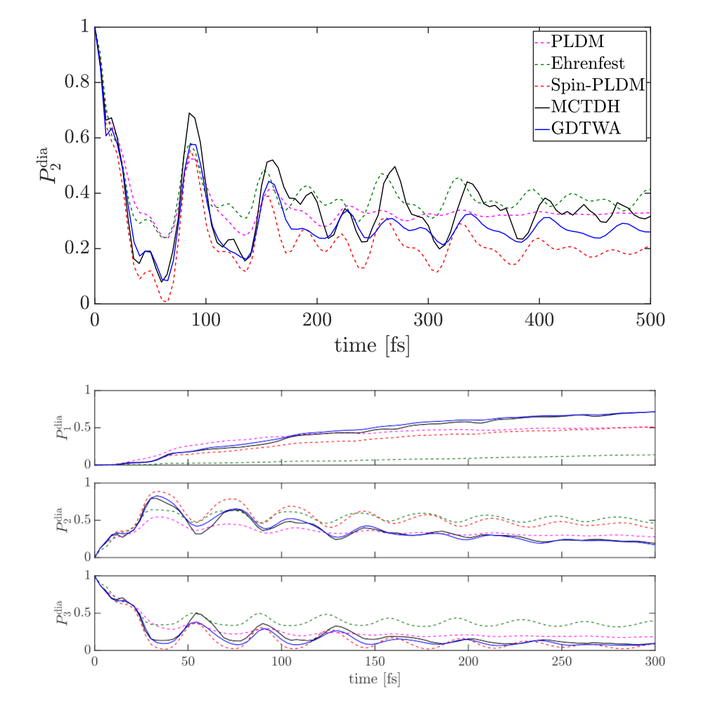
Nonadiabatic molecular dynamics occur in a wide range of chemical reactions and femtochemistry experiments involving electronically excited states. These dynamics are hard to treat numerically as the system’s complexity increases and it is thus desirable to have accurate yet affordable methods for their simulation. Here, we introduce a linearized semiclassical method, the generalized discrete truncated Wigner approximation (GDTWA), which is well-established in the context of quantum spin lattice systems, into the arena of chemical nonadiabatic systems. In contrast to traditional continuous mapping approaches, e.g. the Meyer-Miller-Stock-Thoss and the spin mappings, GDTWA samples the electron degrees of freedom in a discrete phase space, and thus forbids an unphysical unbounded growth of electronic state populations. The discrete sampling also accounts for an effective reduced but non-vanishing zero-point energy without an explicit parameter, which makes it possible to treat the identity operator and other operators on an equal footing. As numerical benchmarks on two Linear Vibronic Coupling models show, GDTWA has a satisfactory accuracy in a wide parameter regime, independently of whether the dynamics is dominated by relaxation or by coherent interactions. Our results suggest that the method can be very adequate to treat challenging nonadiabatic dynamics problems in chemistry and related fields.