From non-Hermitian linear response to dynamical correlations and fluctuation–dissipation relations in quantum many-body systems

Popular summary

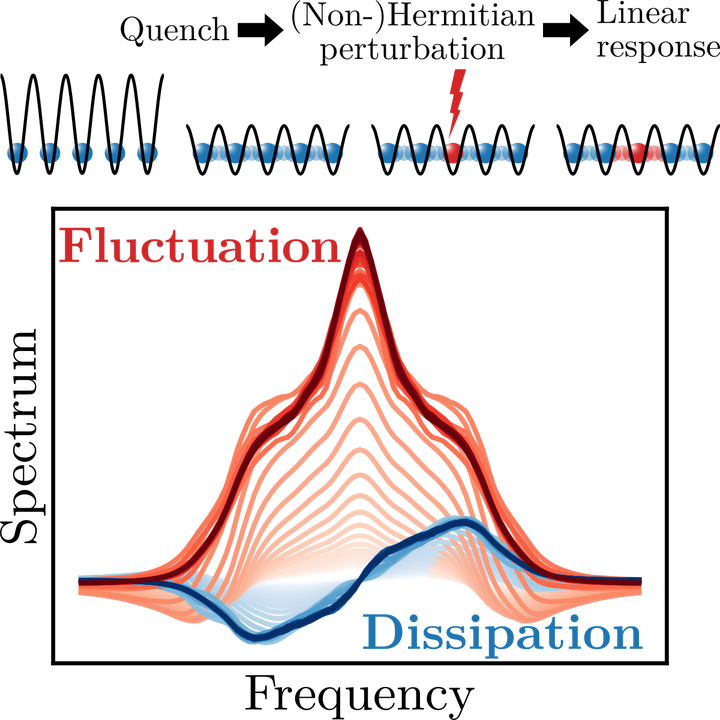
The so-called fluctuation–dissipation relation deeply connects a system’s intrinsic fluctuations on the one hand with the way how it dissipates energy imparted from an external stimulus on the other. Yet, despite being one of the fundamental concepts of statistical mechanics, it has never been directly certified in a quantum system. While there exist standard techniques to measure the dissipation side by probing the linear response to an external perturbation, the fluctuation side is much more challenging. A main obstacle is that it requires knowledge about the correlations between observables at different times. However, in a quantum system, a measurement at one time collapses the wave function, preventing an unperturbed second measurement at a later time.

Here, we propose a method to measure unequal-time correlations as relevant for the fluctuation side and thus to test the fluctuation–dissipation relation. The key is to engineer a perturbation such that it induces an effective loss of probability, mathematically described by a so-called non-Hermitian Hamiltonian. In our work, we propose concrete schemes to effectively realize such non-Hermitian systems in quantum simulators with a focus on cold-atom setups. We demonstrate through extensive numerical simulations how the extracted fluctuation–dissipation relations can help answering the outstanding question of how and to what extent isolated quantum systems locally return to thermal equilibrium.

Our proposed physical realization of effective non-Hermitian dynamics opens up new routes to exploring the exotic realm of non-Hermitian physics as well as characterizing strongly correlated matter and quantum devices via dynamical correlations.