Abstract
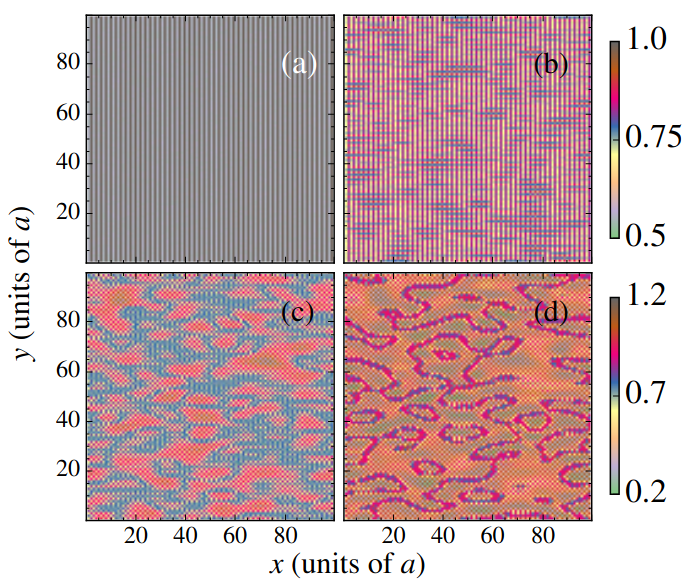
We investigate the quench dynamics of the dipolar bosons in two dimensional optical lattice of square geometry using the time dependent Gutzwiller method. The system exhibits different density orders like the checkerboard and the striped pattern, depending upon the polarization angle of the dipoles. We quench the hopping parameter across the striped density wave (SDW) to striped supersolid (SSS) phase transition, and obtain the scaling laws for the correlation length and topological vortex density, as function of the quench rate. The results are reminiscent of the Kibble-Zurek mechanism (KZM). We also investigate the dynamics from the striped supersolid phase to the checkerboard supersolid phase, obtained by quenching the dipole tilt angle $\theta$. This is a first order structural quantum phase transition, and we study the non-equilibrium dynamics from the perspective of the KZM. In particular, we find the number of the domains with checkerboard order follows a power law scaling with the quench rate. This indicates the applicability of the KZM to this first order quantum phase transition.
