Unveiling Eigenstate Thermalization for Non-Hermitian systems

Abstract

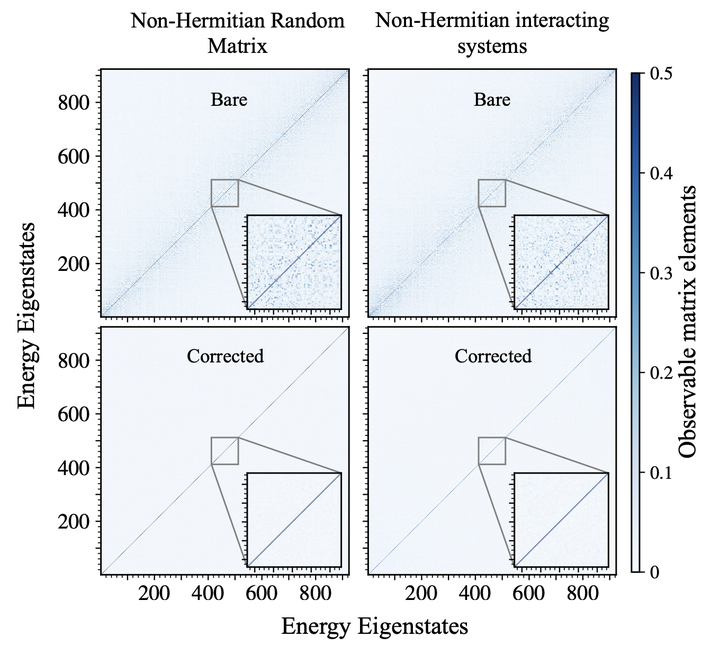
The eigenstate thermalization hypothesis (ETH) has been highly influential in explaining thermodynamic behavior of closed quantum systems. As of yet, it is unclear whether and how the ETH applies to non-Hermitian systems. Here, we introduce a framework that extends the ETH to non-Hermitian systems, within which expectation values of local operators reproduce statistical and scaling predictions known from Hermitian ETH. We illustrate the validity of the framework on non-Hermitian random-matrix and Sachdev-Ye-Kitaev models. Further, we show numerically how the static ETH predictions become imprinted onto the dynamics of local observables. Finally, we present a prescription for observing both ETH-obeying and ETH-violating regimes in an optical-lattice experiment that implements a disordered interacting Hatano-Nelson model. Our results generalize the celebrated ETH to the non-Hermitian setting, and they show how it affects the system dynamics, and how the salient signatures can be observed in present-day cold-atom experiments.