Quantum approximate optimization algorithm for qudit systems

Abstract

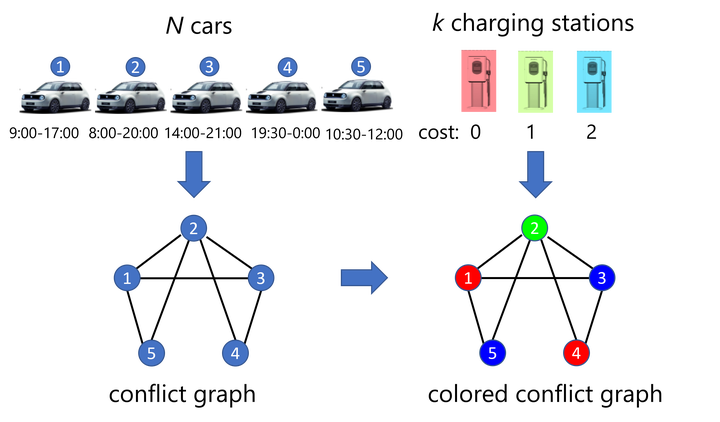
A frequent starting point of quantum computation platforms is the two-state quantum system, i.e., the qubit. However, in the context of integer optimization problems, relevant to scheduling optimization and operations research, it is often more resource-efficient to employ quantum systems with more than two basis states, so-called qudits. Here, we discuss the quantum approximate optimization algorithm (QAOA) for qudit systems. We illustrate how the QAOA can be used to formulate a variety of integer optimization problems such as graph coloring problems or electric vehicle charging optimization. In addition, we comment on the implementation of constraints and describe three methods to include these in a quantum circuit of a QAOA by penalty contributions to the cost Hamiltonian, conditional gates using ancilla qubits, and a dynamical decoupling strategy. Finally, as a showcase of qudit-based QAOA, we present numerical results for a charging optimization problem mapped onto a maximum-$k$-graph-coloring problem. Our work illustrates the flexibility of qudit systems to solve integer optimization problems.